Type `hinf' on command prompt of Matlab.
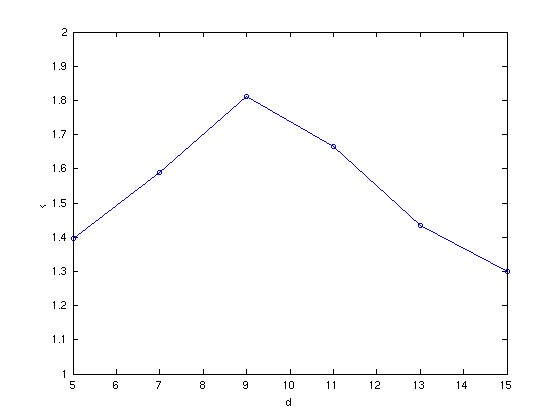
A H_infinity controller is automatically obtained maximizing the variable k by searching constant scaling d in the specified range.
>> hinf d = 5.000000, k = 5.050000 ... infeasible d = 5.000000, k = 2.575000 ... infeasible d = 5.000000, k = 1.337500 ... feasible d = 5.000000, k = 1.956250 ... infeasible d = 5.000000, k = 1.646875 ... feasible d = 5.000000, k = 1.801562 ... feasible d = 5.000000, k = 1.878906 ... feasible d = 5.000000, k = 1.917578 ... infeasible d = 5.000000, k = 1.898242 ... infeasible d = 5.000000, k = 1.888574 ... feasible d = 7.000000, k = 5.050000 ... infeasible d = 7.000000, k = 2.575000 ... infeasible (中略) d = 15.000000, k = 1.724219 ... feasible d = 15.000000, k = 1.762891 ... infeasible d = 15.000000, k = 1.743555 ... infeasible d = 15.000000, k = 1.733887 ... feasible points completed.... 1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17. 18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35. 36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53. 54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71. 72.73.74.75.76.77.78.79.80.81.82.83.84.85.86.87.88.89. 90.91.92.93.94.95.96.97.98.99.100.101.102.103.104.105.106.107. 108.109.110.111.112.113.114.115.116.117.118.119.120.121.122.123.124.125. 126.127.128.129.130.131.132.133.134.135.136.137.138.139.140.141.142.143. 144.145.146.147.148.149.150.151.152.153.154.155.156.157.158.159.160.161. 162.163.164.165.166.167.168.169.170.171.172.173.174.175.176.177.178.179. 180.181.182.183.184.185.186.187.188.189.190.191.192.193.194.195.196.197. 198.199.200.201.202.203.204.205.206.207.208.209.210.211.212.213.214.215. 216.217.218.219.220.221.222.223.224.225.226.227.228.229.230.231.232.233. 234.235.236.237.238.239.240.241.242.243.244.245.246.247.248.249.250.251. 252.253.254.255.256.257.258.259.260.261.262.263.264.265.266.267.268.269. 270.271.272.273.274.275.276.277.278.279.280.281.282.283.284.285.286.287. 288.289.290.291.292.293.294.295.296.297.298.299.300.
Otherwise, change the searching range and/or step of d appropriately as bellow, and design controller again.
Edit the line which specifies the searching range for d in the file hinf.m by the text editor Xemacs.
.... % Specify searching range for constant scaling d dk_hist = []; k_opt_global = 0; for d = 5:2:15 % Edit this line % maximization of k by bisection method k_opt_local = 0; k_low = 0.1; k_high = 10.; .....In the above example, d is set to be 5 initially, then it increases 2 by 2 up to 15.
The state space representation of the controller which achieves the largest value of k (d = 11 in the above example) is automatically stored in the data file `controller.dat'.
This file will be used in the control experiment later.
hinf.m を動かすと,上のグラフの他に,補償器の Bode 線図と,閉ループ系の最大特異値のグラフが表示されます.
これらは,後に行う消音制御の結果に関連しています.
以下,考察を行う際の参考にしてください.
- 補償器の Bode 線図
例:
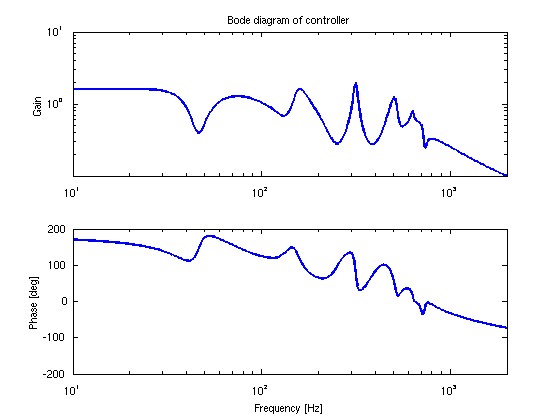
ゲイン特性にはいくつかピークがありますが,これらと Gzw, Gzu, Gyw, Gyu との関連はどうなっているでしょうか?
(このような複雑な補償器は,PID 制御では得ることができません(補償器の次数が足りない).
このような複雑な補償器が自動的に得られることが H∞ 制御の一つの利点です.)
- 閉ループ伝達関数の最大特異値
閉ループ伝達関数を Gcl(s) とすると, 閉ループ伝達関数の最大特異値 = |Gcl(jω)| です. ただし,ω = 2πf, f は周波数でグラフの横軸です.
Gcl(s) は,周波数応答実験で測定した 4 つの「真の」伝達関数 Gzw(s), Gzu(s), Gyw(s), Gyu(s) と,補償器 K(s) を用いて, 以下で与えられます:Gcl(s) = Gzw(s) + Gzu(s) Gyw(s) K(s) / (1 - Gyu(s) K(s)) ω を振ったときの |Gcl(jω)| の最大値が,閉ループ系の H∞ ノルムです.
例:
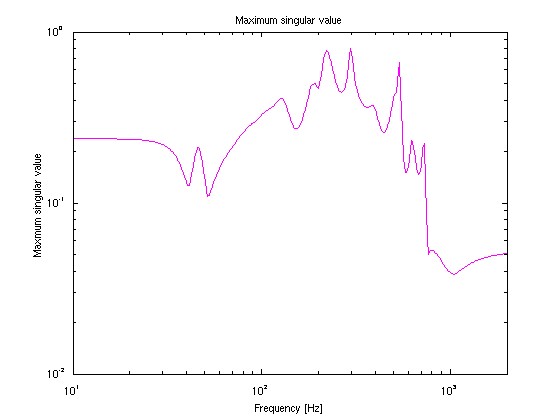
閉ループ系の H∞ ノルムが 1 未満となるように補償器を設計しているので,補償器が正しく設計された場合には,周波数によらず最大特異値は 1 未満となります.
上のグラフでは,最大特異値は 0.8 以下になっており,1 との間にギャップがあります.このような場合は,スケーリング d をもっと細かく変化させ,より大きな k を達成する補償器が存在します.
また,上のグラフでは,約 300Hz で最大特異値が最も大きくなっています.経験的には,この周波数付近で重み W(s) ができるだけ小さくなるように設定すれば,さらに k を大きくすることができ,制御性能が向上します.