一般化プラントデータを作成する

1. nominal.m を実行する．
   
   つぎのように入力してください:

   >> nominal
       

   周波数応答実験の結果を近似して，4 つの伝達関数 Gzw(s), Gyw(s), Gzu(s), Gyu(s) を求め，その Bode 線図を周波数応答実験結果に重ねて表示します．
   実験点(青)と近似曲線(赤)が大体重なっていることを確認してください．
   約 40Hz 以下の低周波域と約 400Hz 以上の高周波域では，両者は重なっていなくても構いません．
   
   
   実行例:
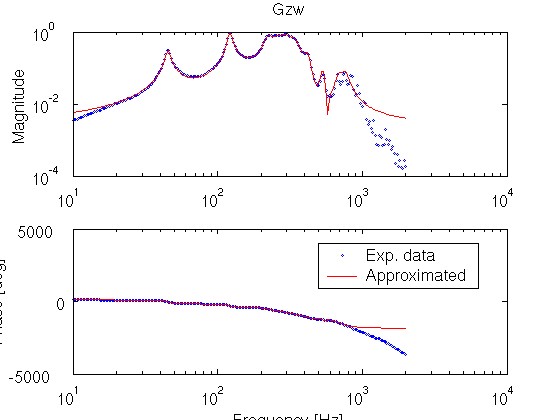
   Gzw の周波数応答(実験結果，青点)とノミナルモデルの Bode 線図
   
   
   Gzw の周波数応答(実験結果，青点)とノミナルモデルの Bode 線図
   
   
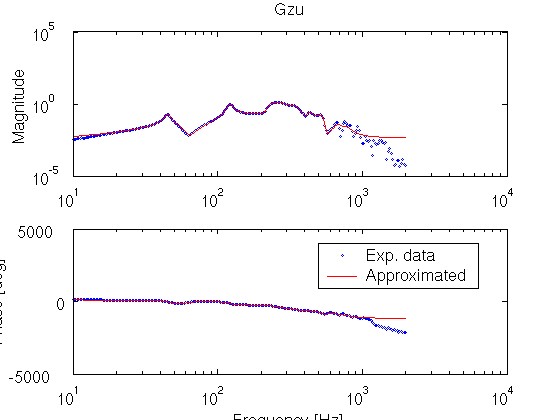
   Gzw の周波数応答(実験結果，青点)とノミナルモデルの Bode 線図
   
   
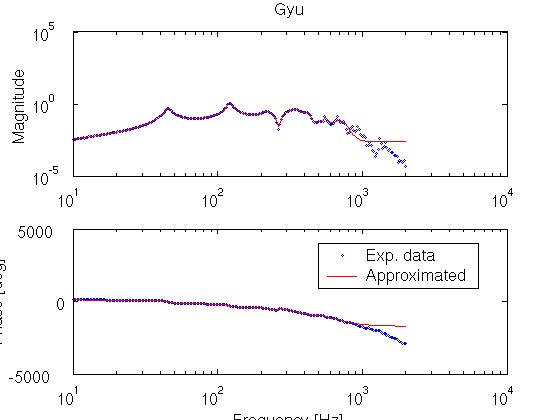
   Gzw の周波数応答(実験結果，青点)とノミナルモデルの Bode 線図
   
   
2. weight.m を実行する
   
   つぎのように入力してください:

   >> weight
       

   Gyu(s) のモデル化誤差と重み関数のゲイン特性が表示されます．
   
   
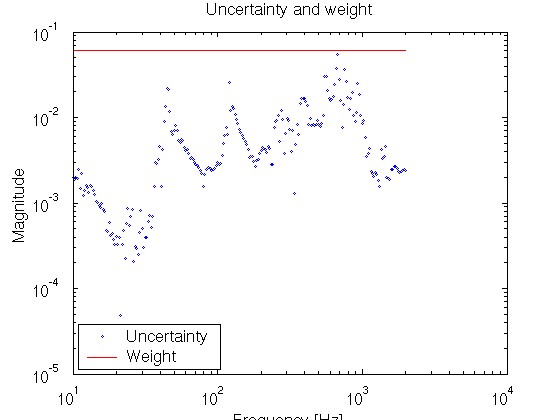
   加法的摂動と重み関数のゲイン特性
   
   このグラフを見て，重み関数のパラメータを調節します．
   重み関数のゲイン(赤線)が，モデル化誤差(青点)を タイトに上から覆うように 重み関数のパラメータを調整してください．
   すき間をあけすぎると，制御性能を良くすることができません．
   逆にモデル化誤差よりも重み関数が小さくなってしまうと， 制御系が不安定になることがあるので注意してください．
   
   具体的には， ファイル weight.m の以下の部分をテキストエディタで編集します．
   
   

   %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
   % 加法的摂動の重み関数を設定 %
   %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
   w0 = 0.016;
   w1 = 2*pi*60;
   w2 = 2*pi*400;
   W = nd2sys(w0*w2*[1, w1], w1*[1, w2]);
   	

   上の例では，以下のように W(s) を設定しています:
   
   W(s) = w0 w2 (s + w1) / (w1 (s + w2))
   
   nd2sys の第一引数 w0*w2*[1, w1] が W(s) の分子多項式を表し， 第二引数 w1*[1, w2] が分母多項式を表しています．