まず,周波数応答データの読み込みます:
>> load spk1.dat注意:
「>>」は入力する必要はありません.Matlab のプロンプトです.
実際に読み込まれたことを確認します.
見やすいように指数表示にしてから spk1 の内容を表示します:
>> format short e >> spk1 ans = 1.0000e+01 5.8768e-04 1.4745e+02 8.6876e-04 1.6989e+02 1.0471e+01 4.7654e-04 1.4666e+02 1.0431e-03 1.6208e+02 1.0965e+01 7.4107e-04 -2.2723e+02 1.1267e-03 -2.0344e+02 1.1482e+01 7.1716e-04 -2.1929e+02 1.2773e-03 -2.0144e+02 1.2023e+01 9.2359e-04 1.3304e+02 1.4885e-03 1.5287e+02 1.2589e+01 9.1276e-04 1.2684e+02 1.6918e-03 1.4954e+02 1.3183e+01 1.0547e-03 -2.3451e+02 1.9434e-03 -2.1453e+02 1.3804e+01 1.1024e-03 1.2155e+02 2.2507e-03 1.4110e+02 1.4454e+01 1.1892e-03 1.2158e+02 2.5899e-03 1.3916e+02 1.5136e+01 1.4463e-03 -2.4348e+02 3.0333e-03 -2.2394e+02 (中略) 1.2023e+03 1.4368e-03 1.4637e+01 2.5930e-03 2.0614e+02 1.2589e+03 8.6975e-04 -1.9890e+01 3.4250e-03 -1.7094e+02 1.3183e+03 9.9568e-04 2.2794e+02 4.3315e-04 8.9225e+01 1.3804e+03 1.1055e-03 1.7386e+02 2.0125e-03 1.7387e+02 1.4454e+03 1.3002e-03 7.6828e+00 6.5796e-04 6.3891e+01 1.5136e+03 1.3388e-03 2.3266e+02 1.2286e-03 6.0970e+01 1.5849e+03 1.0311e-03 1.2270e+02 1.6596e-03 7.9986e+01 1.6596e+03 4.2806e-04 3.5013e+01 4.2572e-04 8.3348e+01 1.7378e+03 2.4791e-04 -8.2351e+01 3.7587e-04 -6.9418e+00 1.8197e+03 3.3969e-04 -2.5462e+02 4.3694e-04 -2.9834e+01 1.9055e+03 3.2147e-04 -3.3319e+01 1.7681e-04 -4.8122e+015 列あって,一列目は周波数[Hz],
2,3 列目は w から z までの周波数応答のゲインおよび位相,
4,5 列目は w から y までの周波数応答のゲインおよび位相,
です.
今計算結果と比較しようとしているのは w から y までの周波数応答のゲイン特性なので,spk1 の 1 列目を横軸に対して 4 列目を縦軸に表示します.
>> loglog(spk1(:,1),spk1(:,4),'.-') >> grid onloglog は両対数プロット,'.-' は,点を実線でつないでプロットするという意味です.
グラフの上向きピークの周波数が共振周波数で,逆に下向きピークの周波数が反共振周波数です.
実行例:

ツールバーにある Zoom in/Zoom out ボタンを使って, 共振周波数と反共振周波数を低い方からそれぞれ 2 つずつ読みとってください.
実行例(一個目の共振周波数を拡大表示したところ):
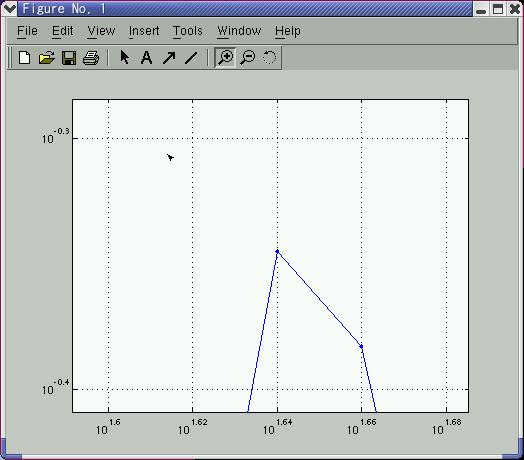
この場合は,つぎのように入力すれば,10 の 1.64 乗を計算することができます.
>> 10^1.64 ans = 4.3652e+01注意:
「^」 はべき乗の意味です.
同様にして,以下の表をうめてください:
| 1次 | 2次 | |
| 共振周波数 | 44 Hz | ? Hz |
| 反共振周波数 | ? Hz | ? Hz |
- 開口端の場合(今回の実験の場合)
片端開口の場合の共振周波数(fr とします)と反共振周波数(fa とします)は,それぞれ,
fr = (2m+1)c / (4L)
fa = mc / (2L)
で与えられます.
ここで,m = 0, 1, 2, ... で,L は管の全長 [m],c は音速 [m/sec] です.
- 閉口端の場合
この場合は,fa, fr は次のように与えられます.
fr = mc / (2L)
fa = (2m+1)c / (4L)
開口端の場合と比べると,fr, fa が入れ替わっていることに注意してください.
実際にメジャーで L を測り, Matlab 上で fr, fa を 計算して以下の表を埋めてください.
(Matlab 上で計算できます)
なお,音速 c は 340[m/sec] としてください.
| m = 0 | m = 1 | m = 2 | |
| 共振周波数(fr) | ? Hz | ? Hz | ? Hz |
| 反共振周波数(fa) | ? Hz | ? Hz | ? Hz |