


Next: 5 消音制御実験
Up: Text
Previous: 3.2 モデル化誤差とロバスト制御
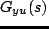 のモデル化誤差を考慮することにより,
問題1をつぎのように書き替えることができる.
のモデル化誤差を考慮することにより,
問題1をつぎのように書き替えることができる.
問題 2
任意の
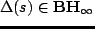
に対して,
図
2の閉ループ系を内部安定化し,かつ,
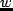
から
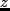
までの閉ループ伝達関数の
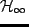
ノルムを最小化する
補償器
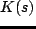
を求めよ.
ここで,
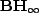 は,
は,
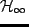 ノルムが
ノルムが 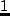 以下の,安定な伝達関数の集
合である.
また,
以下の,安定な伝達関数の集
合である.
また,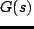 は,
は,
![$\displaystyle G(s) = \left[\begin{array}{@{\:}cc@{\:}} \bar G_{zw}(s) & \bar G_{zu}(s) \\ \bar G_{yw}(s) & G_{yu}(s) \end{array}\right]$](img44.png) |
(6) |
で与えられる.
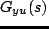
は (
4)式で与えられる.
このような,モデル化誤差に対するロバスト安定性と制御性能の最適化を同時
に図る補償器設計問題は,ロバスト性能問題と呼ばれ,
現実の制御対象に対する補償器設計問題としてよく現れる.
この問題の直接的な解法は知られていないが,
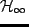 制御問題の解法を利用して補償器設計を行うことができる.
制御問題の解法を利用して補償器設計を行うことができる.
問題2の閉ループ系から摂動 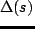 を上に引き出して,
を上に引き出して,
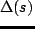 を取り除くと,図4の閉ループ系が得られる.
を取り除くと,図4の閉ループ系が得られる.
さらに,スケーリングと呼ばれる変数を導入することにより,
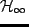 制御問題の解法を繰り返し利用して解くことが可能な次の設計問題を
得る.
制御問題の解法を繰り返し利用して解くことが可能な次の設計問題を
得る.
問題 3 (定数スケールド
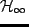
制御問題)
図
5の閉ループ系を内部安定化し,
かつ,閉ループ伝達関数のノルムを
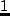
未満とする
補償器
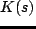
および正数
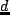
を求めよ.
さらに,解が存在する範囲で,正数
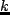
を最大化せよ.
図:
定数スケールド
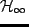 制御問題
制御問題
|
|
課題 6
問題
3を解き,補償器を求めよ.
開ループおよび閉ループ特性のゲイン特性を比較し,
得られた補償器で達成される消音制御性能を予測せよ.



Next: 5 消音制御実験
Up: Text
Previous: 3.2 モデル化誤差とロバスト制御
Yasuhide Kobayashi
平成15年4月8日
![]() のモデル化誤差を考慮することにより,
問題1をつぎのように書き替えることができる.
のモデル化誤差を考慮することにより,
問題1をつぎのように書き替えることができる.
![]() は,
は,
![]() ノルムが
ノルムが ![]() 以下の,安定な伝達関数の集
合である.
また,
以下の,安定な伝達関数の集
合である.
また,![]() は,
は,
![$\displaystyle G(s) = \left[\begin{array}{@{\:}cc@{\:}} \bar G_{zw}(s) & \bar G_{zu}(s) \\ \bar G_{yw}(s) & G_{yu}(s) \end{array}\right]$](img44.png)
![]() 制御問題の解法を利用して補償器設計を行うことができる.
制御問題の解法を利用して補償器設計を行うことができる.
![]() を上に引き出して,
を上に引き出して,
![]() を取り除くと,図4の閉ループ系が得られる.
を取り除くと,図4の閉ループ系が得られる.
![]() 制御問題の解法を繰り返し利用して解くことが可能な次の設計問題を
得る.
制御問題の解法を繰り返し利用して解くことが可能な次の設計問題を
得る.