


Next: 3.2 モデル化誤差とロバスト制御
Up: 3 モデリング
Previous: 3 モデリング
未知システムの伝達関数(以下,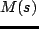 とする)を同定するための手法の一つ
として,
周波数応答法がある.
周波数応答法では,未知システムにある周波数
とする)を同定するための手法の一つ
として,
周波数応答法がある.
周波数応答法では,未知システムにある周波数 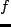 の正弦波
の正弦波 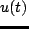 を入力
し,その出力
を入力
し,その出力 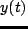 を観測する.
未知システムの非線形性が弱く,ほぼ線形系とみなせるような場合には,
出力信号
を観測する.
未知システムの非線形性が弱く,ほぼ線形系とみなせるような場合には,
出力信号 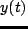 も同一周波数
も同一周波数 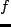 の正弦波となり(図3),
未知システムの伝達関数
の正弦波となり(図3),
未知システムの伝達関数 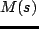 は,入出力信号の振幅比(出力/入力)
は,入出力信号の振幅比(出力/入力) 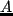 と
位相差(入力に対する出力の進み)
と
位相差(入力に対する出力の進み) 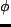 によって,
によって,
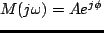 |
(3) |
と特徴づけられる.
周波数 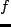 を細かく変化させながら,振幅比
を細かく変化させながら,振幅比 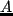 と位相差
と位相差 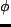 を記録し,
プロットしたものが,未知システムの周波数応答であり,
これを最小二乗法等を用いて近似することにより,
未知システムの伝達関数
を記録し,
プロットしたものが,未知システムの周波数応答であり,
これを最小二乗法等を用いて近似することにより,
未知システムの伝達関数 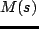 を決定することができる.
を決定することができる.
課題 1
周波数応答法により,図
1の 4 つの伝達関数
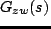
,
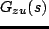
,
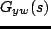
,
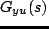
を求めよ.
課題 2
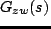
の周波数応答をプロットし,主な共振周波数および反共振周波
数を列挙せよ.これらを,理論式による計算結果と比較・検討せよ.
各課題に対する作業手順の詳細は,以下の URL を参照のこと:
http://multi2.nagaokaut.ac.jp/~kobayasi/ANC/



Next: 3.2 モデル化誤差とロバスト制御
Up: 3 モデリング
Previous: 3 モデリング
Yasuhide Kobayashi
平成15年4月8日
![]() とする)を同定するための手法の一つ
として,
周波数応答法がある.
周波数応答法では,未知システムにある周波数
とする)を同定するための手法の一つ
として,
周波数応答法がある.
周波数応答法では,未知システムにある周波数 ![]() の正弦波
の正弦波 ![]() を入力
し,その出力
を入力
し,その出力 ![]() を観測する.
未知システムの非線形性が弱く,ほぼ線形系とみなせるような場合には,
出力信号
を観測する.
未知システムの非線形性が弱く,ほぼ線形系とみなせるような場合には,
出力信号 ![]() も同一周波数
も同一周波数 ![]() の正弦波となり(図3),
未知システムの伝達関数
の正弦波となり(図3),
未知システムの伝達関数 ![]() は,入出力信号の振幅比(出力/入力)
は,入出力信号の振幅比(出力/入力) ![]() と
位相差(入力に対する出力の進み)
と
位相差(入力に対する出力の進み) ![]() によって,
によって,